The guardian of our night skies never fails to mesmerize us with the wonders its capable of through its perfectly timed and relatively simple motions. Lets start with the phases of the moon – did you know that inspite of the moon orbiting around the earth and rotating on its axis we always see the same side of the moon, its due to this phenomenon called tidal locking which we will probably dive into later in part II.
Phases
Ancient humans used the phases of moon to keep track of days and seasons – that’s actually where our division of months also comes from as a lunar cycle is ~29.5 days
Why this happens?
Moon shines because of the sun light it reflects, as moon orbits around the earth, the position of the moon changes both with respect to Earth and the sun – this leads to part of the luminated side of the moon to be visible to us – these are called the phases of the moon
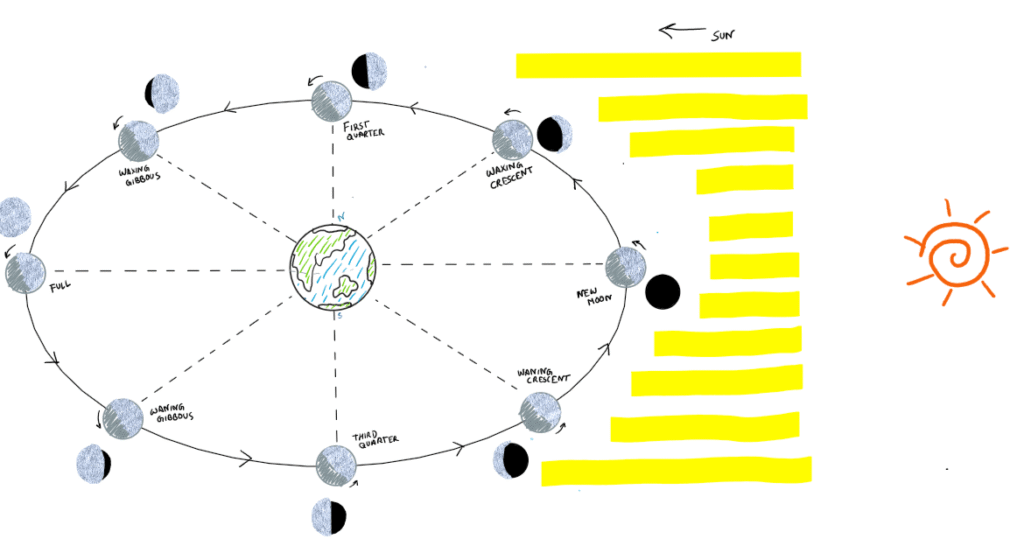
Figure 1 – Phases of moon
In Figure 1 above, we see how moon goes from a full moon when its directly between sun and earth to a full moon being on the other side with the illuminated part being visible to us increasing day by day (waxing) to a full moon and then decreasing (waning) and back to a new moon.
Orbit
Interestingly enough the orbit of moon is not perfectly circular either, its elliptical leadinf to a perigee (closest point to the earth – where moon appears bigger – supermoon) and an apogee where moon appears smaller.
The moon takes 27 days to orbit the earth (note lunar cycle is 29.5 days) – the difference here is because of earth’s movement around the sun
There is also a precessional motion noticed in the moon every ~8.85 years where the axis change directions (orbit rotates)
Moon’s orbit is also tilted with respect to earth and this tilt varies from 5-5.3 degrees (averaged around 5.1 degrees) – because of the gravitational effect of sun. This precesses over 18.6 year cycle
And moon is also not perpendicular to its orbit, its tilted by about 6.68 degrees towards its orbital plane around earth
In addition to that every year moon moves 3.8cm away from us. We’ll do a separate article diving into details of orbital mechanics of the moon as it is quite interesting on its own.
Solar Eclipse
Solar eclipse occurs when moon lies on thw same line between earth and sun, blocking out the light of sun (partially or fully) from earth.
The different types of solar eclipses are categorized as total (moon covers the sun completely), partial (moon covers only part of the sun), annular (apparent size of the moon is smaller – and leaves a ring)
Its important to note that eclipses are based on 3 bodies – a light emitting, a light blocking and an observing body.
These eclipse models are geocentric since we make our observations from earth.
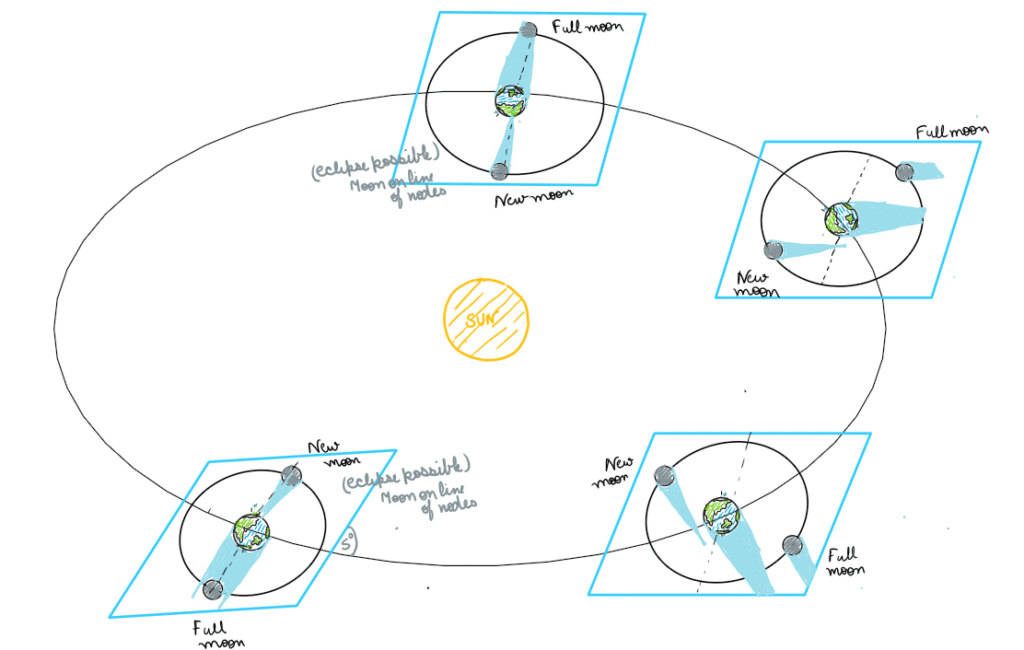
Figure 2 – Line of nodes
Figure 2 above shows some different possible positions of earth, moon and sun system – even though there’re different possibilities of a new moon and full mon, an eclipse only occurs when moon is said to be along the line of nodes (moon is between the earth and the sun), solar eclipse occurs when moon is said to be a new moon – illuminated side facing away from us
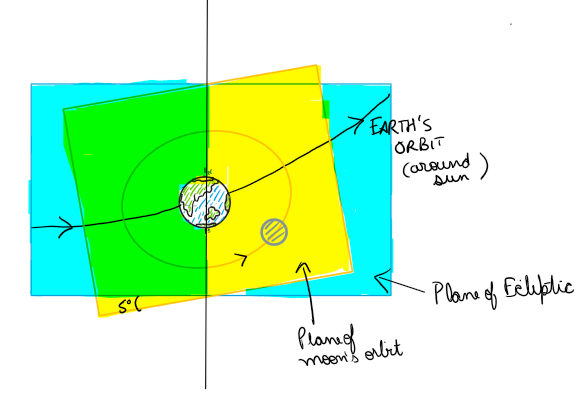
Figure 3 – Moon’s orbit
Lunar Eclipse
Continuing from what was said above a lunar eclipse will occur when moon is a full moon and along the line of nodes (earth is directly between the sun and moon)
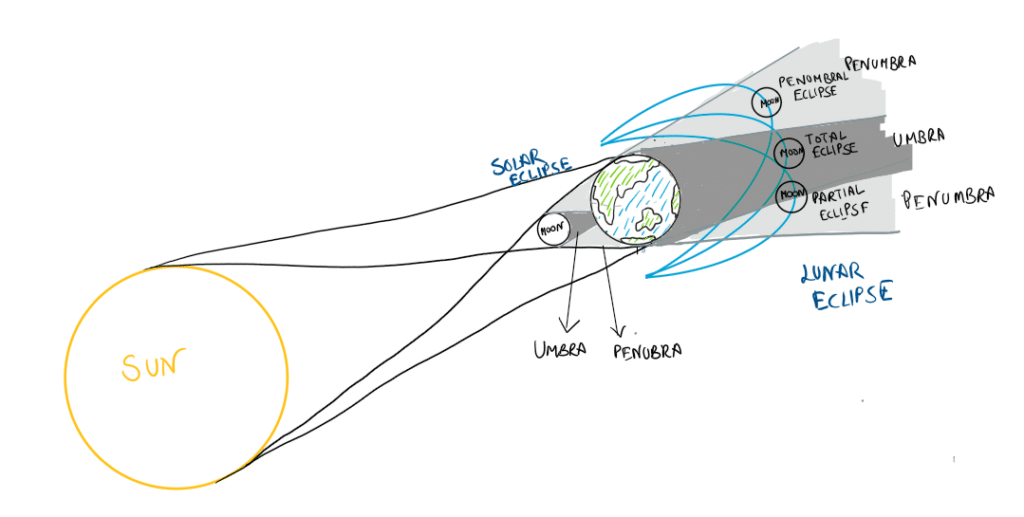
Figure 4 – Umbra and Penumbra
Figure 4 above shows both solar and lunar eclipse. For lunar eclipse, the eclipse is categorized in different types:
- total lunar eclipse occurs when the moon is completely in earth’s shadow (umbra – dark central part) – this is when the moon often appears to have a reddish tint – because some sunlight from the edges of earth reaches to illuminate the moon – this light passes through the earth’s atmosphere which scatters most of the blue light (scattering follows an inverse relation with wavelength – longer wavelengths like red scattering less) leaving mostly red light to reach the moon.
- partial lunar eclipse is said to occur when moon is partially in the umbral region
- penumbral lunar eclipse occurs when moon pases through the penumbral (outer lighter region) of earth’s shadow
Calculating Eclipse
https://github.com/w-winnie/livnlearn/blob/main/eclipses_livnlearnversion.ipynb
In this notebook we try and calculate when does an eclipse occur based on observational data (position of sun, moon and earth) obtained from spicepy package –
more information about it can be found here – https://naif.jpl.nasa.gov/naif/aboutspice.html
To summarize this notebook – we aim to findwhen did an eclipse (solar/lunar) occur in a given duration using the position of sun and moon
We get radius of Moon and sun (planetary constants) and positional data (ephemeris) from NASA’s SPICE python package
then we calculate vectors for these objects from our point of observation and find the angular separation of the two objects and their angular size as seen from our point of observation
using their separation and size we calculate an overlap fraction and classify the eclipse
Imports¶
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import numpy as np
import math
# https://naif.jpl.nasa.gov/naif/aboutspice.html
import spiceypy as spice
Constants¶
DEG = 180.0/np.pi #degrees #spice angles are in radians
MU_SUN = 1.32712440018e11 #km^3/s^2 #standard gravitational parameter of Sun
Get Data¶
We load 3 files,
leap seconds file (to find the time eclipse in earth times – as the clocks get corrected sometimes),
planetary constants (for radius of planets so we can calculate apprent sizes) and
ephemeris data (to find position of different celestial bodies)
# https://naif.jpl.nasa.gov/pub/naif/generic_kernels/pck/
# https://naif.jpl.nasa.gov/pub/naif/generic_kernels/lsk/
def load_kernels():
spice.furnsh("../data/naif0012.tls") # Leap seconds - conversion of earth time to ephemeris time
spice.furnsh("../data/de440s.bsp") # Ephemeris data - position and velocities
spice.furnsh("../data/pck00011.tpc") # Planetary constants - radius, spin axes, rotation rates etc.
Get Apparent Distance between objects – Angle between 2 Vectors¶
This method defines how to get an angle between two vectors through a dot product – this gives us apparant separation between two celestial bodies as seen from a third body
(e.g. we can take position of sun and moon as seen from earth – calculate the vectors and the angular separation between sun and moon as seen from earth)
def get_angle_between_vectors(v1, v2):
v1 = np.array(v1, dtype=float)
v2 = np.array(v2, dtype=float)
dot = np.dot(v1, v2)
norm1 = np.linalg.norm(v1)
norm2 = np.linalg.norm(v2)
if norm1 == 0 or norm2 == 0:
raise ValueError("One of the vectors has zero length")
cos_theta = dot / (norm1 * norm2)
cos_theta = np.clip(cos_theta, -1.0, 1.0)
return np.arccos(cos_theta)
# return spice.vsep(v1, v2)
Get Apparent Size – Angular Radius¶
this method helps us determine how big a body of given radius looks from given distance by a second body
def get_angular_radius(radius_km, dist_km):
x = max(0.0, min(1.0, radius_km / max(dist_km, 1e-9)))#values clamped [0,1]
return math.asin(x)
Get Radius¶
This method basically gets object radius from SPICE
SPICE stores 3 radii (across x, y, z) – as things are not perfect spheres
so we take a mean of the 3
# https://naif.jpl.nasa.gov/pub/naif/toolkit_docs/IDL/icy/cspice_bodvrd.html
def get_mean_radius_km(body_name):
radii = spice.bodvrd(body_name.upper(), "RADII", 3)[1]
return float(np.mean(radii))
Get State Vector¶
State vectors basically a vector concatenating position and velocity of a body in 3 cartesian coordinates w.r.t. another body
This method uses the SPICE library to pass in object codes and get a vector representing the position and velocities of the bodies
# codes for solar system bodies
# 10 - Sun, 399 - Earth, 301 - Moon
# https://naif.jpl.nasa.gov/pub/naif/toolkit_docs/C/req/naif_ids.html#Planets%20and%20Satellites
def get_state_vec(targ, obs, et, ref="J2000"):
state, lt = spice.spkgeo(targ=targ, et=et, ref=ref, obs=obs)
return np.array(state[:3])
Get Angular Separation¶
This method uses the above defined method to get the of sun and moon as observed from earth – at each point of time in a given time range
def solar_moon_separation_over_range(start_date, end_date, step_hours=6):
ets, seps_deg, dates = [], [], []
t = start_date
while t <= end_date:
et = spice.utc2et(t.strftime("%Y-%m-%dT%H:%M:%S"))
r_es = get_state_vec(10, 399, et) # target sun 10 wrt Earth 399
r_em = get_state_vec(301, 399, et) # target moon 301 wrt Earth 399
sep = get_angle_between_vectors(r_es, r_em) * DEG
ets.append(et); seps_deg.append(sep); dates.append(t)
t += timedelta(hours=step_hours)
return np.array(ets), np.array(seps_deg), dates
Get Eclipse overlap¶
This method calculates overlap between two objects by comparing their angular (apparent) separation and their angular (apparent) size
def circle_overlap_fraction(target_r, eclipsing_body_r, center_dist, eps=1e-12):
r1, r2, d = float(target_r), float(eclipsing_body_r), float(center_dist)
#distance between circles centers is greater than sum of radius (no touch)
if d >= r1 + r2:
return 0.0
#distance between circles is greater than diff of radius (total eclipse)
# target body inside eclipsing body - eclipsing body is larger
if d <= abs(r2 - r1) and r2 >= r1:
return 1.0
#distance between circles is less than diff of radius (partial eclipse on target)
#eclipsing body inside target - eclipsing body is smaller
if d <= abs(r2 - r1) and r2 < r1:
return (math.pi * r2**2) / (math.pi * r1**2)
# Partial overlap
# law of cosines (angles at which circles intersect))
c1 = (d**2 + r1**2 - r2**2) / (2*d*r1 + eps)
c2 = (d**2 + r2**2 - r1**2) / (2*d*r2 + eps)
c1 = max(-1.0, min(1.0, c1)) # clip to [-1,1] to avoid fp issues
c2 = max(-1.0, min(1.0, c2))
# area of circular segments
a1 = r1**2 * math.acos(c1)
a2 = r2**2 * math.acos(c2)
# area of triangle formed by circles centers and intersection points (Heron's)
a3 = 0.5 * math.sqrt(max(0.0, (-d+r1+r2)*(d+r1-r2)*(d-r1+r2)*(d+r1+r2)))
overlap_area = a1 + a2 - a3
target_area = math.pi * r1**2
return max(0.0, min(1.0, overlap_area / (target_area + eps)))
Get Gamma¶
This is a metric I added to compare with NASA’s catalog metrics as seen here – https://eclipse.gsfc.nasa.gov/SEgoogle/SEgoogle2021.html
this metric indicates the offset of the eclipse from earth’s center
def compute_gamma_at_time(et):
r_es = get_state_vec(10, 399, et) # Sun wrt Earth
r_em = get_state_vec(301, 399, et) # Moon wrt Earth
# Shadow axis direction at the Moon toward the sun in the Earth frame
u = r_es - r_em # vector Moon - Sun in Earth frame
u = u / np.linalg.norm(u) # unit direction
# Closest vector from the line (through r_em along u) to Earth's center (origin):
# v = - u × (r_em × u)
v = -np.cross(u, np.cross(u, r_em))
# Sign: north (+) if v has positive component along J2000 +Z (Earth's north)
sign = np.sign(np.dot(np.array([0.0, 0.0, 1.0]), v))
Re_eq = get_mean_radius_km(body_name="EARTH")
gamma = sign * (np.linalg.norm(v) / Re_eq)
return gamma
Get Metrics¶
Algorithm –
1 – Get Data
1.1 – Get Radius of Moon and sun rom NASA’s SPICE python package (planetary constants)
1.2 – Get Sun and Moon positional data from NASA’s SPICE python package (ephemeris)
2 – Calculate position vectors for Sun and Moon wrt to Earth => (r_es, r_em)
3 – Calculate the distance of sun & moon from earth => (d_es, d_em)
4 – Calculate apparent size (angular radii) of sun and moon as seen from earth using their size R_sun, R_moon and distance from earth d_es, d_em => (a_sun, a_moon)
4 – Calculate apparent separation between sun and moon as seen from earth using r_es and r_em => (sep)
5 – Calculate fraction of overlap by comparing angular size of sun and moon a_sun, a_moon and their angular separation sep as seen from the earth => (frac)
6 – Classify
def get_solar_metrics_at_time(et):
# radius of sun and moon in km
R_sun = get_mean_radius_km("SUN")
R_moon = get_mean_radius_km("MOON")
R_earth = get_mean_radius_km("EARTH")
#position vectors for sun and moon wrt earth
r_es = get_state_vec(10, 399, et)
r_em = get_state_vec(301, 399, et)
# distance of sun and moon from earth
d_es = np.linalg.norm(r_es)
d_em = np.linalg.norm(r_em)
# apparent angular radius (size) of sun and moon from earth
a_sun = get_angular_radius(R_sun, d_es)
a_moon = get_angular_radius(R_moon, d_em)
# apparent distance between sun and moon from earth
sep = get_angle_between_vectors(r_es, r_em) #Only from geocenter
# Anywhere from earth - Lunar horizontal parallax ≈ asin(R_earth / d_em) (~57 arcmin)
pi_E = math.asin(min(1.0, R_earth / max(d_em, 1e-9)))
# We can reduce the geocenter separation by at most pi_E by choosing an optimalobserver on Earth's surface
sep_global = max(0.0, sep - pi_E)
# fraction of Sun's disk covered (planar small-angle approx)
frac = circle_overlap_fraction(a_sun, a_moon, sep_global)
if sep_global <= abs(a_moon - a_sun):
if a_moon > a_sun: #if moon looks bigger than sun
kind = "total"
elif a_moon < a_sun: #if moon looks smaller than sun
kind = "annular"
else:
kind = "exactly equal angular sizes"
elif frac > 0: # partial eclipse
kind = "partial"
else:
kind = "no eclipse"
gamma = compute_gamma_at_time(et)
return {
"sun_obscuration_fraction": frac,
"sep_deg": sep * DEG,
"alpha_sun_deg": a_sun * DEG,
"alpha_moon_deg": a_moon * DEG,
"classification": kind,
"gamma": gamma
}
The calculation of lunar eclipse is similar to that of a solar one – the only difference is we change our point of observation to be on the moon and then calculate overlap between earth and sun
def get_lunar_metrics_at_time(et):
# radius of sun and moon in km
R_earth = get_mean_radius_km("EARTH")
R_sun = get_mean_radius_km("SUN")
R_moon = get_mean_radius_km("MOON")
# position vectors for sun and earth wrt moon
r_em = get_state_vec(301, 399, et) # Moon wrt Earth
r_es = get_state_vec(10, 399, et) # Sun wrt Earth
r_ms = get_state_vec(10, 301, et) # Sun wrt Moon
d_ms = np.linalg.norm(r_ms)
d_me = np.linalg.norm(r_em)
# apparent angular radius (size) of sun and earth from moon
a_E = get_angular_radius(R_earth, d_me)
a_S = get_angular_radius(R_sun, d_ms)
# shadow angular radii (radians) (angular size of earth - sun)
a_umb = max(0.0, a_E - a_S)
a_pen = a_E + a_S
# in km
r_umb = d_me * math.tan(a_umb)
r_pen = d_me * math.tan(a_pen)
# offset between earth and sun poditiond from moon (radians)
theta = get_angle_between_vectors(r_em, -r_ms)
# in km
s = d_me * theta
# fractions of the Moon's disk covered
frac_umb = circle_overlap_fraction(R_moon, r_umb, s) if r_umb > 0 else 0.0
frac_pen = circle_overlap_fraction(R_moon, r_pen, s)
# along diameter - negative umbral magnitude => no umbral contact; >1 => total (Moon fully within umbra)
umbral_mag = (r_umb + R_moon - s) / (2.0 * R_moon)
penumbral_mag = (r_pen + R_moon - s) / (2.0 * R_moon)
if frac_umb >= 1.0:
kind = "total lunar eclipse (Moon fully in umbra)"
elif frac_umb > 0:
kind = "partial lunar eclipse (Moon partially in umbra)"
elif frac_pen > 0:
kind = "penumbral lunar eclipse (Moon only in penumbra)"
else:
kind = "no lunar eclipse"
return {
"umbra_fraction_of_moon": frac_umb,
"penumbra_fraction_of_moon": frac_pen,
"theta_deg": theta * DEG,
"alpha_earth_deg": a_E * DEG,
"alpha_sun_deg": a_S * DEG,
"classification": kind,
"umbral_magnitude": umbral_mag,
"penumbral_magnitude": penumbral_mag,
}
Get Eclipse Candidate in a time period¶
Now we just loop over a time period
this loop also contains a condition to find duration and peak of the eclipse
def scan_solar_eclipses(start_dt, end_dt, step_size, min_obsc=0.01):
t = start_dt
events = []
active = False
current = None
while t <= end_dt:
et = spice.utc2et(t.strftime("%Y-%m-%dT%H:%M:%S"))
m = get_solar_metrics_at_time(et)
if m["sun_obscuration_fraction"] >= min_obsc:
if not active:
active = True
current = {"start": t, "peak": (t, m), "peak_val": m["sun_obscuration_fraction"], "min_gamma": (t, m["gamma"], abs(m["gamma"]))}
else:
if m["sun_obscuration_fraction"] > current["peak_val"]:
current["peak"] = (t, m)
current["peak_val"] = m["sun_obscuration_fraction"]
if abs(m["gamma"]) < current["min_gamma"][2]:
current["min_gamma"] = (t, m["gamma"], abs(m["gamma"]))
elif active:
current["end"] = t
events.append(current)
active = False
t += step_size
if active:
current["end"] = end_dt
events.append(current)
return events
def scan_lunar_eclipses(start_dt, end_dt, step_size, min_umb_or_pen=0.01):
t = start_dt
events = []
active = False
current = None
while t <= end_dt:
et = spice.utc2et(t.strftime("%Y-%m-%dT%H:%M:%S"))
m = get_lunar_metrics_at_time(et)
measure = max(m["umbra_fraction_of_moon"], m["penumbra_fraction_of_moon"])
if measure >= min_umb_or_pen:
if not active:
active = True
current = {"start": t, "peak": (t, m), "peak_val": measure}
else:
if measure > current["peak_val"]:
current["peak"] = (t, m)
current["peak_val"] = measure
elif active:
current["end"] = t
events.append(current)
active = False
t += step_size
if active:
current["end"] = end_dt
events.append(current)
return events
RUN¶
load_kernels()
start = datetime(2024, 1, 1)
end = datetime(2026, 12, 31)
step_size_solar = timedelta(minutes=5)
step_size_lunar = timedelta(hours=1)
solar_events = scan_solar_eclipses(start, end, step_size_solar, min_obsc=0.01)
print("SOLAR ECLIPSE CANDIDATES:")
for ev in solar_events:
peak_t, peak_m = ev["peak"]
print(f"{ev['start']} → {ev['end']} | peak @ {peak_t} | obsc={peak_m['sun_obscuration_fraction']:.3f} | {peak_m['classification'] }| gamma={peak_m['gamma']:.3f}")
lunar_events = scan_lunar_eclipses(start, end, step_size_lunar, min_umb_or_pen=0.01)
print("LUNAR ECLIPSE CANDIDATES:")
for ev in lunar_events:
peak_t, peak_m = ev["peak"]
print(f"{ev['start']} → {ev['end']} | peak @ {peak_t} | "
f"umbra={peak_m['umbra_fraction_of_moon']:.3f}, pen={peak_m['penumbra_fraction_of_moon']:.3f} | {peak_m['classification']}| umbral_mag={peak_m['umbral_magnitude']:.3f}, penumbral_mag={peak_m['penumbral_magnitude']:.3f}")
SOLAR ECLIPSE CANDIDATES: 2024-04-08 15:45:00 → 2024-04-08 20:55:00 | peak @ 2024-04-08 16:40:00 | obsc=1.000 | total| gamma=-1.006 2024-10-02 15:50:00 → 2024-10-02 21:50:00 | peak @ 2024-10-02 16:55:00 | obsc=0.846 | annular| gamma=0.996 2025-03-29 08:55:00 → 2025-03-29 12:45:00 | peak @ 2025-03-29 10:50:00 | obsc=0.939 | partial| gamma=1.042 2025-09-21 17:35:00 → 2025-09-21 21:55:00 | peak @ 2025-09-21 19:45:00 | obsc=0.804 | partial| gamma=-1.067 2026-02-17 10:00:00 → 2026-02-17 14:30:00 | peak @ 2026-02-17 12:40:00 | obsc=0.922 | annular| gamma=-1.005 2026-08-12 15:40:00 → 2026-08-12 20:00:00 | peak @ 2026-08-12 17:00:00 | obsc=1.000 | total| gamma=1.000 LUNAR ECLIPSE CANDIDATES: 2024-03-25 05:00:00 → 2024-03-25 10:00:00 | peak @ 2024-03-25 07:00:00 | umbra=0.000, pen=0.962 | penumbral lunar eclipse (Moon only in penumbra)| umbral_mag=-0.161, penumbral_mag=0.924 2024-09-18 01:00:00 → 2024-09-18 05:00:00 | peak @ 2024-09-18 03:00:00 | umbra=0.014, pen=1.000 | partial lunar eclipse (Moon partially in umbra)| umbral_mag=0.046, penumbral_mag=0.997 2025-03-14 05:00:00 → 2025-03-14 10:00:00 | peak @ 2025-03-14 06:00:00 | umbra=0.676, pen=1.000 | partial lunar eclipse (Moon partially in umbra)| umbral_mag=0.671, penumbral_mag=1.750 2025-09-07 16:00:00 → 2025-09-07 21:00:00 | peak @ 2025-09-07 17:00:00 | umbra=0.467, pen=1.000 | partial lunar eclipse (Moon partially in umbra)| umbral_mag=0.505, penumbral_mag=1.486 2026-03-03 09:00:00 → 2026-03-03 15:00:00 | peak @ 2026-03-03 10:00:00 | umbra=0.059, pen=1.000 | partial lunar eclipse (Moon partially in umbra)| umbral_mag=0.121, penumbral_mag=1.151 2026-08-28 02:00:00 → 2026-08-28 07:00:00 | peak @ 2026-08-28 03:00:00 | umbra=0.249, pen=1.000 | partial lunar eclipse (Moon partially in umbra)| umbral_mag=0.323, penumbral_mag=1.356
References
https://science.nasa.gov/moon/moon-phases
https://science.nasa.gov/moon/tidal-locking
https://svs.gsfc.nasa.gov/5326
https://eclipse.gsfc.nasa.gov/LEdecade/LEdecade2021.html
https://eclipse.gsfc.nasa.gov/SEgoogle/SEgoogle2021.html
